Vous êtes ici : Département PhysiqueFR
- Partager cette page :
- Version PDF
Spin-Hall Effect including screening: presence of longitudinal pure spin-current
Jean-Éric Wegrowe
Laboratoire des solides irradiés (LSI)
École Polytetchnique, CNRS, CEA, Palaiseau
le 18 octobre 2022
Mardi 18 octobre 2022 à 10 h 30
Bâtiment Fermat
Salle F-4109
Salle F-4109
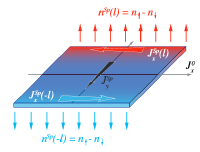
Spin-accumulation can be produced at the edges of a conducting bar by injecting an electric current into a non-magnetic material with high spin-orbit coupling. This effect is called Spin Hall Effect (SHE). It is easy to understand the SHE intuitively in the framework of the two-spin-channel model, as it is simply the classical Hall effect applied to each spin channel. This simple intuitive description will be presented and discussed. The global picture (see figure below) should be understandable without any preliminary knowledge about spin-dependent transport phenomena.
However - from a more quantitative point of view - an important difficulty arises in the formal description, which is the same as for the classical Hall effect: it is due to the fact that the amount of electric charges accumulated at the edges of the Hall bar is not directly imposed by the external constraints but by the system itself, in reaction to the current injection and the effective magnetic field (like for the Le Chatelier-Lenz principle). As a consequence, since the quantitative determination of the solution of the spin-dependent drift-diffusion equations necessitates local boundary conditions, this determination is problematic.
We show that the problem can be solved on the basis of a least dissipation principle [1-4]. The global constraints are then used instead of the missing local boundary conditions. The minimization of the dissipation functionnal - under the approximation of both weak and strong spin-flip scattering - leads to analytical expressions of the spin-currents and spin- accumulation.
[1] M. Creff et al., Surface current in Hall devices, J. Appl. Phys 128, 054501 (2020)
[2] F. Faisant et al., The physical properties of the Hall current, J. Appl. Phys. 129, 144501 (2021)
[3] P.-M. Déjardin and J-E. Wegrowe, Stochastic description of the stationary Hall effect, J. Appl. Phys. 128, 184504 (2020)
[4] M. Creff, E. Olive, and J.-E. Wegrowe, Screening effect in Spin-Hall Devices, Phys. Rev. B 105, 174419 (2022).
However - from a more quantitative point of view - an important difficulty arises in the formal description, which is the same as for the classical Hall effect: it is due to the fact that the amount of electric charges accumulated at the edges of the Hall bar is not directly imposed by the external constraints but by the system itself, in reaction to the current injection and the effective magnetic field (like for the Le Chatelier-Lenz principle). As a consequence, since the quantitative determination of the solution of the spin-dependent drift-diffusion equations necessitates local boundary conditions, this determination is problematic.
We show that the problem can be solved on the basis of a least dissipation principle [1-4]. The global constraints are then used instead of the missing local boundary conditions. The minimization of the dissipation functionnal - under the approximation of both weak and strong spin-flip scattering - leads to analytical expressions of the spin-currents and spin- accumulation.

[1] M. Creff et al., Surface current in Hall devices, J. Appl. Phys 128, 054501 (2020)
[2] F. Faisant et al., The physical properties of the Hall current, J. Appl. Phys. 129, 144501 (2021)
[3] P.-M. Déjardin and J-E. Wegrowe, Stochastic description of the stationary Hall effect, J. Appl. Phys. 128, 184504 (2020)
[4] M. Creff, E. Olive, and J.-E. Wegrowe, Screening effect in Spin-Hall Devices, Phys. Rev. B 105, 174419 (2022).







